Ejemplo: Determinar el incremento de esfuerzo causado por esta carga debajo del centro de la superficie rectangular.

Una superficie flexible rectangular de 2.5 mX 5 m, está localizada sobre el terreno y cargada con q0 = 145 kN/m2. Determine el incremento de esfuerzo causado por esta carga a una profundidad de 6.25 m debajo del centro de la superficie rectangular Use la carta de Newmark. 

 

FIGURA 4.15

Solución: Aquí, z = 6.25 m, por lo que la longitud AB en la figura 4.14 es 6.25 m. Con esta escala, la planta de la superficie rectangular cargada puede ser dibujada. La figura 4.15 muestra la planta colocada sobre la carta de Newmark con el centro de la superficie cargada arriba del centro de la carta. La razón para la colocación es que el incremento de esfuerzo se requiere en un punto inmediatamente abajo del centro de la superficie rectangular. El número de elementos de la carta de influencia que están dentro de la planta es aproximadamente 26, por lo que 

Incremento del Esfuerzo Debido a Cualquier Tipo de Carga – Debido a una Cimentación.

El incremento de esfuerzo vertical bajo cualquier tipo de superficie flexible cargada es fácilmente determinado con el uso de la carta de influencia de Newmark (1942). En principio, la carta se basa en la ecuación (4.3) para la estimación del incremento de esfuerzo vertical bajo el centro de una superficie circular cargada. De acuerdo con la ecuación (4.3) 

Ahora sustituimos varios valores de Δp/q0 en la ecuación (4.24) para obtener los valores correspondientes de R/z. La tabla 4.4 muestra los valores calculados de R/z para
Δp/q0  = 0, 0.1, 0.2,. . . , 1.

Usando los valores adimensionales de R/z mostrados en la tabla 4.4, dibujemos círculos concéntricos que tienen radios iguales a R/z, como muestra la figura 4.14. Note que la distancia AB en la figura 4.14 es unitaria. El primer círculo es un punto con radio nulo. Similarmente, el segundo círculo tiene un radio de 0.2698 (AB). El último tiene un radio infinito. Esos círculos fueron divididos por líneas radiales igualmente espaciadas, produciéndose lo que se llama carta de Newmark. El valor de influencia, IV, de esta carta es

Para la carta mostrada en la figura 4.14,1V 1/200 = 0.005.

A continuación se da un procedimiento paso a paso para usar la carta de Newmark determinar el esfuerzo vertical bajo una superficie cargada de cualquier forma:

1. Identifique la profundidad z bajo la superficie cargada donde va a determinarse el esfuerzo.

FIGURA 4.14 Carta de influencia para el cálculo de la presión vertical (según Newmark, 1942)

2. Adopte una escala z = AB (es decir longitud unitaria de acuerdo con la carta de Newmark).

3. Dibuje la planta de la superficie cargada con base en la escala adoptada en el paso 2.

4. Coloque la planta dibujada en el paso 3 sobre la carta de Newmark de manera que el punto bajo el cual el esfuerzo va a ser determinado, quede directamente arriba del centro de la carta.

5. Cuente el número de elementos de la carta que caen dentro de la planta. Sean éstos igual a N.

6. Calcule el incremento de esfuerzo como 

Donde q0 = carga por área unitaria sobre la superficie cargada.

Ejemplo: Determinar el incremento promedio del esfuerzo bajo el centro de la superficie cargada

Refiérase a la figura 4.10. Determine el incremento promedio del esfuerzo bajo el centro de la superficie cargada de z = 3 m a z = 5 m (es decir; entre los puntos A yA’).

Solución: Refiérase a la figura 4.10. La superficie cargada se divide en cuatro superficies rectangulares, cada una de 1.5 m X 1.5 m (L x B). Usando la ecuación (4.19), el incremento promedio del esfuerzo (entre las profundidades requeridas) bajo la esquina de cada superficie rectangular se expresa como 

 FIGURA 4.10

Ejemplo: Determinar el Incremento del Esfuerzo Vertical debido a la carga debajo el centro de la superficie rectangular.

Una superficie flexible rectangular mide 5 pies X 10 pies en planta y soporta una carga de 2000 lb/pies2. 

Determine el incremento del esfuerzo vertical debido a la carga a una profundidad de 12.5 pies debajo del centro de la superficie rectangular.

Solución: Reflérase a la figura 4.5. Para este caso 

Calculo Asentamiento Elástico de una Cimentación Superficial Basado en la Teoría de la Elasticidad.

El asentamiento elástico de una cimentación superficial se estima usando la teoría de la elasticidad. Con referencia a la figura 4.16 y aplicando la ley de Hooke, 

FIGURA 4.16 Asentamiento elástico de cimentación Superficial.

Teóricamente, si la profundidad de la cimentación Df = O, H = ∞, y la cimentación es perfectamente flexible, de acuerdo con Harr (1966), el asentamiento se expresa como (figura 4.17)

Los valores de a para varias relaciones longitud a ancho (LIB) se muestran en la figura 4.18. El asentamiento promedio inmediato para una cimentación flexible también se expresa como 

Los valores de α para varias relaciones longitud a ancho (LIB) se muestran en la figura 4.18. El asentamiento promedio inmediato para una cimentación flexible también se expresa como

FIGURA 4.17  Asentamiento elástico de cimentaciones flexibles y rígidas.

La figura 4.18 muestra también los valores de αprom para varias relaciones L/B de una cimentación.

Sin embargo, si la cimentación mostrada en la figura 4.17 es rígida, el asentarniento inmediato será diferente y se expresa como 

Los valores de αr para varias relaciones L/B de cimentaciones se muestran en la figura 4.18.

Si  Df = O y H < ∞ debido a la presencia de una capa rígida (incompresible), como muestra la figura 4.17, 

Las variaciones de F1 y F2 con H/B se dan en las figuras 4.19 y 4.20, respectivamente (Steinbrenner, 1934).

Es también importante ver que las relaciones anteriores para Se suponen que la profundidad de la cimentación es igual a cero. Para Df > O, la magnitud de Se decrecerá. 

 FIGURA 4.19  Variación de F1 con H/B

FIGURA 4.20  Variación de F2 con H/B

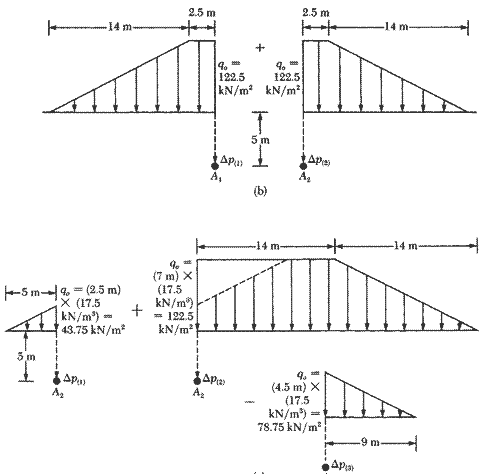
Ejemplo: Determinación del Esfuerzo Bajo el Terraplén.

En la figura 4.13a se muestra un terraplén. Determine el incremento de esfuerzo bajo el terraplén en los puntos A1 y A2.

Solución

FIGURA 1.42  Valor de influencia I’ para la carga del Terraplén

FIGURA 4.13

Incremento del Esfuerzo Bajo un Terraplén - Debido a una Cimentación.

La figura 4.11 muestra la sección transversal de un terraplén de altura H. Para esta condición bidimensional de carga, el incremento del esfuerzo vertical se expresa como

Para una derivación detallada de la ecuación, véase Das (1997). Una forma simplificada de la ecuación (4.20) es 

donde I’ = una función de B1/z y B2/z 

FIGURA 4.11  Carga del Terraplén.

La variación de I’ con B1/z yB2/z se muestra en la figura 4.12. La aplicación de este diagrama se ilustra en este ejemplo.

Incremento del Esfuerzo Vertical Promedio debido a un Área Cargada Rectangularmente debido a una Cimentación.

El incremento del esfuerzo vertical debajo de una esquina de una superficie rectangular cargada uniformemente fue dado por (figura 4.7) 

En muchos casos se requiere determinar el incremento promedio del esfuerzo Δpprom, debajo de una esquina de una superficie rectangular cargada uniformemente con límites de z = O a z = H, como muestra la figura 4.7. 


Esto se evalúa como 

FIGURA 4.7  Incremento del esfuerzo promedio vertical debido a una superficie flexible rectangular cargada

donde: 

La variación de ‘a se muestra en la figura 4.8, según propuesta de Griffiths (1984).

En la estimación del asentamiento bajo una cimentación, se requiere determinar el incremento promedio del esfuerzo vertical en sólo una capa dada; es decir, entre z = H1 y z = H2, como muestra la figura 4.9. Según Griffiths (1984), 

FIGURA 4.8  Factor de Influencia  Ia de Griffiths

FIGURA 4.9  Incremento del promedio de presión entre  z=H1 y z=H2 abajo de la esquina de una superficie rectangular uniformemente cargada.

donde

Incremento del Esfuerzo Vertical en una Masa de Suelo Causado por Carga de la Cimentación – Debajo de un Área Rectangular.

El procedimiento de integración de Ja ecuación de Boussinesq también permite la evaluación del esfuerzo vertical en cualquier punto A debajo de una esquina de una superficie flexible rectangular cargada (figura 4.3). 

Para esto, considere un área elemental 

TABLA 4.1

 FIGURA 4.3  Determinación del esfuerzo debajo de una esquina de una superficie flexible rectangular cargada.

TABLA 4.2

El incremento del esfuerzo en cualquier punto debajo de una superficie rectangular cargada también se encuentra usando la ecuación (4.5) junto con la figura 4.5. Para determinar el esfuerzo a la profundidad z debajo del punto O, divida la superficie cargada en cuatro rectángulos. El punto O es la esquina común a cada rectángulo, luego use la ecuación (4.5) para calcular el incremento del esfuerzo a la profundidad z debajo del punto O causado por cada superficie rectangular. El incremento total del esfuerzo causado por toda la superficie cargada se expresa ahora como 

donde I1,I2, I3 e I 4 = valores de influencia de los rectángulos 1, 2, 3 y 4, respectivamente.

En la mayoría de los casos, el esfuerzo vertical debajo del centro de una superficie rectangular es de importancia, y se da por la siguiente relación: 

FIGURA 4.4

FIGURA 4.5  Esfuerzo debajo de cualquier punto de una superficie rectangular carga.

FIGURA 4.6 Método 2:1 para encontrar el incremento de esfuerzo debajo de una cimentación

Los ingenieros en cimentaciones usan a menudo un método aproximado para determinar el incremento del esfuerzo con la profundidad causado por la construcción de una cimentación, denominado método 2.’l (figura 4.6). De acuerdo con éste, el incremento del esfuerzo a la profundidad z es 

Note que la ecuación (4.14) se basa en la hipótesis de que el esfuerzo se difunde desde la cimentación a lo largo de líneas con una pendiente de 2 vertical a 1 horizontal.