Ejemplo: Determinación de la fuerza activa de Rankine por unidad de longitud del muro antes y después de que ocurra la grieta de tensión.

Un muro de retención de 6 m de altura debe soportar un suelo con peso especifico y = 17.4 kN/m3, un ángulo de fricción Ø = 26° y cohesión c = 14.36 kN/m2. Determine la fuerza activa de Rankine por unidad de longitud del muro antes y después de que ocurra la grieta de tensión y determine la línea de acción de la resultante en ambos casos.

Solución:  Para Ø = 26º

Para la construcción de la mayoría de los muros de retención se usa un relleno granular y c = O. El ejemplo 6.2 es entonces un problema académico; sin embargo, ilustra los principios básicos del cálculo de la presión activa de Rankine.

Presión Activa de Tierra de Rankine.

La condición de la presión lateral de tierra descrita en la sección 6.2 implica muros que no ceden en absoluto. Sin embargo, si un muro tiende a moverse alejándose del suelo una distancia Δx, como muestra la figura 6.7a, la presión del suelo sobre el muro a cualquier profundidad decrecerá. Para un muro sin fricción, el esfuerzo horizontal, σh, a una profundidad z será igual a K0σv, (= K0yz) cuando Δx es cero. Sin embargo, con Δx> O, σh será menor que K0σv.

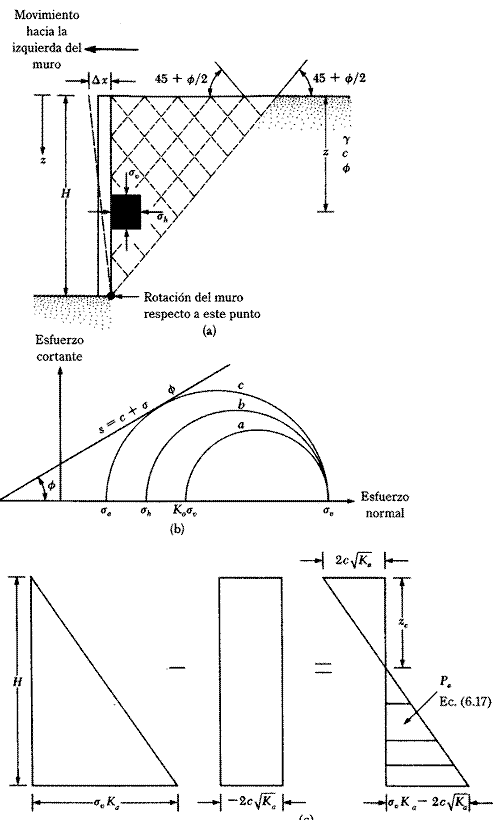
Los círculos de Mohr correspondientes a desplazamientos del muro de Δx = O y Δx > O se muestran por los círculos a y b, respectivamente, en la figura 6.7b. Si el desplazamiento del muro, Δx, continúa creciendo, el correspondiente círculo de Mohr tocará eventualmente la envolvente de falla de Mohr-Coulomb definida por la ecuación 

El círculo marcado con c en la figura 6.7b. Representa la condición de falla en la masa del suelo; el esfuerzo horizontal es igual entonces a c y se denomina presión activa de Rankine. Las líneas de deslizamiento (planos de falla) en el suelo forman entonces ángulos de ±(45 +Ø/2) con la horizontal, como muestra la figura 6.7a.

Refiérase de nuevo a la ecuación (1.84), que relaciona los esfuerzos principales para un círculo de Mohr que toca la envolvente de falla de Mohr-Coulomb: 

 FIGURA 6.7  Presión activa de Rankine.

La variación de la presión activa con la profundidad para el muro mostrado en la figura 6.7a se da en la figura6.7c. Note σv = O en z = O y σv = y H  en z = H.La distribución de presión muestra que en z = O, la presión activa es igual a -2c raizcuadrada(K0), que indica un esfuerzo de tensión, el cual decrece con la profundidad y es cero a la profundidad z = zc, o 

La profundidad zc se llama profundidad de la grieta de tensión, porque el esfuerzo de tensión en el suelo causará eventualmente una grieta a lo largo de la interfaz suelo- muro. La fuerza activa total de Rankine por unidad de longitud del muro antes de que ocurra la grieta de tensión es 

 

TABLA 6.1  Variación del K0 de Rankine.

 

Después de que ocurre la grieta de tensión, la fuerza sobre el muro será causada sólo por la distribución de presión entre las profundidades z = zc y z = H, como muestra el área sombreada en la figura 6.7c. Ésta se expresa como 

Para fines de cálculo en algunos problemas de diseño de muros de retención, un relleno de suelo cohesivo se reemplaza por un suelo supuesto granular con un diagrama de presión activa triangular de Rankine con σ a = O en z = O

 

 en Z = 0

(véase la fIgura 6.8). En tal caso, la fuerza activa supuesta por unidad de longitud de muro es 

 

FIGURA 6.8 Diagrama supuesto de presión activa para un relleno de arcilla detrás de un muro de retención

Sin embargo, la condición de presión activa de la tierra se alcanzará sólo si se permite que el muro “ceda” suficientemente. La cantidad necesaria de desplazamiento hacia afuera del muro es aproximadamente de entre 0.001H y 0.004H para rellenos de suelo granular y aproximadamente de entre 0.01H y 0.04H para rellenos de suelo cohesivo.

Ejemplo: Determinación de la Fuerza latera de la tierra en reposo para un muro.

Para el muro de retención mostrado en la figura 6.6(a), determine la fuerza lateral de la tierra en reposo por unidad de longitud del muro. 

Determine también la posición de la fuerza resultante.

Solución: 

FIGURA 6.6

Presión Lateral de Tierra en Reposo.

Considere un muro vertical de altura H, como muestra la figura 6.3, que retiene un suelo con peso específico de y. Una carga uniformemente distribuida de q/área unitaria, es también aplicada a la superficie del terreno. La resistencia cortante, s, del suelo es 

 FIGURA 6.3  Presión de la tierra en reposo.

A cualquier profundidad z debajo de la superficie del terreno, el esfuerzo vertical es 

Si el muro está en reposo y no se permite que se mueva respecto a la masa del suelo (es decir, deformación horizontal nula), la presión lateral a una profundidad z es

donde

u = presión de poro del agua
K0 = coeficiente de presión de la tierra en reposo

Para un suelo normalmente consolidado, la relación para K0 (Jaky 1944) es 

La ecuación (6.3) es una aproximación empírica.
Para arcillas normalmente consolidadas, el coeficiente de presión de tierra en reposo se aproxima (Brooker y Ireland, 1965) por 

donde Ø =  ángulo de fricción máximo drenado

Con base en los resultados experimentales de Brooker y Ireland (1965), el valor de K0 para arcillas normalmente consolidadas es aproximado en relación con el índice de plasticidad (PI):

Para arcillas preconsolidadas,

donde OCR = tasa de preconsolidación

Mayne y Kulhawy (1982) analizaron los resultados de 171 suelos diferentes probados en laboratorio. Con base en este estudio, ellos propusieron una relación empírica general para estimar la magnitud de K0 para arena y arcilla: 

En la figura 6.4, OCR es el valor de OCR en el punto B.

Con un valor seleccionado apropiadamente del coeficiente de presión de tierra en reposo, la ecuación (6.2) se usa para determinar la variación de la presión lateral de la tierra con la profundidad z. La figura 6.3b exhibe la variación de σh con la profundidad para el muro mostrado en la figura 6.3a. Note que si la sobrecarga q = O y la presión de poro u= O, el diagrama de presión será un triángulo. La fuerza total, P0, por unidad de longitud del muro dado en la figura 6.3a ahora se obtiene del área del diagrama de presión dado en la figura 6.3b como 

FIGURA 6.4  Historia del esfuerzo de un suelo bajo condición K0

donde

P1 = área del rectángulo 1
P2 = área del triángulo 2

La localización de la línea de acción de la fuerza resultante, P, se logra tomando momentos respecto al fondo del muro. Entonces, 

Si el nivel freático está a una profundidad z <H, el diagrama de presión en reposo mostrado en la figura 6.3b tendrá que ser modificado un poco, como muestra la figura 6.5. Si el peso específico efectivo del suelo debajo del nivel freático es

Note que en estas ecuaciones, σ’v  σ’h y son las presiones efectivas vertical y horizontal. La determinación de la distribución de presión total sobre el muro requiere añadir la presión hidrostática. La presión hidrostática, u, es cero de z = O a z = H1 en z = H2, u = H2 y2. La variación de σ’h y u con la profundidad se muestra en la figura 6.5b. Por lo tanto, la fuerza total por longitud unitaria del muro se determina del área del diagrama de presión. Se obtiene entonces 

 

donde A = área del diagrama de presión.

 FIGURA 6.5

Entonces, 

Sherif y otros (1984) demostraron por medio de varías pruebas de modelos que la ecuación (6.3) da buenos resultados para estimar la presión lateral de la tierra en reposo para arenas sueltas. Sin embargo, para arena densa compactada, subestima considerablemente el valor de K0. Por esta razón, ellos propusieron una relación modificada para K0:

Presión Lateral de Tierra

Los taludes verticales o casi verticales de suelo son soportados por muros de retención, tablaestacas en voladizo vertical, ataguías de tablaestacas, cortes apuntalados y otras estructuras similares. El adecuado diseño de esas estructuras requiere la estimación de la presión lateral de la tierra, que es una función de varios factores, tales como: (a) el tipo y magnitud del movimiento de los muros, (b) los parámetros de resistencia cortante del suelo, (c) el peso específico del suelo y (d) las condiciones de drenaje en el relleno. La figura 6.1 muestra un muro de retención de altura H. Para tipos similares de relleno:

a. muro está restringido contra movimiento (figura 6.lb). La presión lateral de la tierra sobre el muro a cualquier profundidad se llama presión de la tierra en reposo.

b. muro se inclina respecto al suelo retenido (figura 6.lb). Con suficiente inclinación del muro, fallará una cuña triangular de suelo detrás del muro. La presión lateral para esta condición se llama presión activa de la tierra.

c. El muro es empujado hacia el suelo retenido (figura 6.lc). Con suficiente movimiento del muro, fallará una cuña de suelo. La presión lateral para esta condición se llama presión pasiva de la tierra. 

La figura 6.2 muestra la naturaleza de la variación de la presión lateral (σh) a cierta profundidad sobre el muro con la magnitud del movimiento de éste. 

FIGURA 6.1  Naturaleza de la presión lateral de la tierra sobre un muro de retención.

FIGURA 6.2 Naturaleza de la variación de la presión lateral de la tierra a una cierta profundidad

En las siguientes secciones veremos varias relaciones para determinar las presiones en reposo, activa y pasiva sobre un muro de retención. Se supone que el lector ya conoce el concepto de presión lateral en suelos, por lo que este capítulo servirá como repaso.

Ejemplo: Determinación del valor del coeficiente de reacción del subsuelo segun las dimensiones de una cimentación.

De una prueba de placa de carga (dimensiones de la placa: 1 pie X 1 pie) en el campo, se determinó que el coeficiente de reacción del subsuelo en un suelo arenoso es de 80 lb/pulg3. (a) ¿Cuál será el valor del coeficiente de reacción del subsuelo sobre el mismo suelo para una cimentación con dimensiones de 30 pies X 30 pies? (b) Si la cimentación tiene dimensiones de 45 pies X 30 pies, ¿cuál será el valor del coeficiente de reacción del subsuelo?

Solución:

Parte a

De la ec. (5.46), 

Ejemplo: Verificación si laspresiones del Suelo son menores que la capacidad de carga neta admisible - Losas

La planta de una losa de cimentación con cargas de columnas se muestra en la figura 5.12. Use la ecuación (5.25) para calcular las presiones del suelo en los puntos A, B, C, D, E, F, G, H, I,J, K, L, M y N. El tamaño de la losa es de 76 pies X 96 pies, todas las columnas son de 24 pulg X 24 pulg en sección transversal y = 1.5 klb/pies2. Verifique que las presiones del suelo son menores que la capacidad de carga neta admisible.

Solución: De la figura 5.12,

Carga muerta de columnas (DL)= 100 + 180 + 190 + 110 + 180 + 360 + 400 + 200 + 190 + 400 + 440 + 200 + 120 + 180 + 180 + 120 =  3550 Klb
Carga viva de columnas (LL) = 60 + 120 + 120 + 70 + 120 + 200 + 250 + 120 + 130 +240+300+120+70+120+120+70 = 2230 Klb

Por lo que

Carga de servicio = 3550 + 2230 = 5780 Klb

De acuerdo con el ACI 318-95 (sección 9.2), carga factorizada, U = (1.4) (Carga muerta) + (1.7)(Carga viva). Entonces,

Carga factorizada = (1.4)(3550) + (1.7)(2230) = 8761 klb-

Los momentos de inercia de la cimentación son 

Nota DL = carga muerta

         LL = carga viva

Figura 5.12  Planta de una losa de cimentación.

Las presiones del suelo en todos  los puntos son menores que el valor dado qadm(neta)= 1.5 Klb/pies^2

Coeficiente κ para cimentaciones sobre arcillas.

La definición de k en la ecuación (5.47) es la misma que la de la ecuación (5.45). En unidades inglesas,

Las definiciones de k y k1 son las mismas que las de la ecuación (5.46). 

Para cimentaciones rectangulares con dimensiones B x L (para suelo y q similares) 

donde k = coeficiente del módulo del subsuelo de la cimentación rectangular (LXB)
k(BXB) = coeficiente del módulo del subsuelo de una cimentación cuadrada con dimensiones B X B

La ecuación (5.49) indica que el valor de k para una cimentación muy larga con ancho B es aproximadamente O,67k(BxB).
El módulo de elasticidad de los suelos granulares crece con la profundidad. Como el asentamiento de una cimentación depende del módulo de elasticidad, el valor de k crece conforme aumenta la profundidad de la cimentación.

La tabla siguiente da algunos rangos típicos del valor para el coeficiente de reacción k1 del subsuelo para suelos arenosos y arcillosos. 

Scott (1981) propuso que para suelos arenosos el valor de k0.3 se obtenga de la resistencia por penetración estándar a cualquier profundidad dada, o 

donde Ncor = resistencia a la penetración estándar corregida.

En unidades inglesas, 

Para vigas largas, Vesic (1961) propuso una ecuación para estimar la reacción del subsuelo: 

El coeficiente de reacción del subsuelo es también un parámetro muy útil en el diseño de pavimentos rígidos de carreteras o aeropistas. El pavimento con una superficie de desgaste de concreto se llama generalmente pavimento rígido y con una superficie de desgaste asfáltica se llama pavimento flexible. Para una carga de superficie que actúa sobre un pavimento rígido, el esfuerzo de tensión máximo ocurre en la base de la losa. Para estimar la magnitud del esfuerzo de tensión horizontal máximo desarrollado en la base del pavimento rígido, son sumamente útiles las soluciones elásticas para losas sobre cimentaciones Winkler. Parte de este trabajo inicial fue hecho por Westergaard (1926, 1939, 1947).

Ahora que hemos analizado el coeficiente de reacción del subsuelo, procederemos con el análisis del método flexible aproximado de diseño de losas de cimentación. Este método, tal como es propuesto por el Comité 336(1988) del American Concrete Institute, será descrito paso a paso. El procedimiento de diseño se basa principalmente en la teoría de placas. Su uso permite que los efectos (es dech momento, fuerza cortante y deflexión) de una carga concentrada de columna sean evaluados. Si las zonas de influencia de dos o más columnas se cruzan, se usa la superposición para obtener el momento, fuerza cortante y deflexión netos en cualquier punto.

1. Suponga un espesor, h, para la losa de acuerdo con el paso 6 como se hizo en el método rígido convencional. (Nota: h es el espesor total de la losa)

2. Determine la rigidez por flexión R de la losa: 

donde 

EF = módulo de elasticidad del material de la cimentación

μF = relación de Poisson del material de la cimentación

3. Determine el radio de la rigidez efectiva: 

donde k = coeficiente de la reacción del subsuelo

La zona de influencia de cualquier carga de columna será del orden de 3 a 41).

4. Determine el momento (en coordenadas polares en un punto) causado por una carga de columna (figura 5.11a):

Las variaciones de A1 y A2 con r/L’ se muestran en la figura 5.llb (véanse los detalles en Hetenyi, 1946).
En el sistema coordenado cartesiano (figura 5.lla), 

FIGURA 5.11  Método flexible aproximado para el diseño de losas

5. Para un ancho unitario de losa, determine la fuerza cortante, V, causada por una carga de columna: 

La variación de A3 con r/L’ se muestra en la figura 5.11b.

6. Si el borde de la losa se localiza en la zona de influencia de una columna, determine el momento y la fuerza cortante a lo largo de la cuña (suponga que la losa es continua). Momento y fuerza cortante opuestos en signo a los determinados son aplicados a los bordes para satisfacer las condiciones conocidas.

7. La deflexión (S) en cualquier punto es dada por

La variación de A4 se da en la figura 5.11.