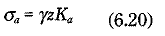Juntas en la Construcción de Muros de Retención.

Un muro de retención se construye con una o más de las siguientes juntas:

1. Juntas de construcción (figura 7.2la) son juntas verticales y horizontales que se colocan entre dos coladas sucesivas de concreto. Para incrementar el cortante en las juntas deben usarse ranuras o muescas. Si no se usan, la superficie de la primera colada debe limpiarse y dársele una textura rugosa antes de la siguiente colada de concreto.

2. juntas de contracción (figura 7.21b) son juntas verticales (ranuras) colocadas en la fachada de un muro (desde la parte superior de losa de base a la parte superior del muro) que permiten que el concreto se contraiga sin daño aparente. Las ranuras deben ser de 0.25 a 0.3 pulg ( 6 a 8 mm) de ancho y de 0.5 a 0.6 pulg (=12 a 16 mm) de profundidad, aproximadamente. 

FIGURA 7.22 Estabilidad de un muro de retención bajo fuerzas sísmicas

donde γ = peso específico del relleno; 

y

Para una derivación detallada de la ecuación (7.28), véase Das (1983).

Con base en las ecuaciones (7.2 7) y (7.28), el siguiente procedimiento se usa para determinar el peso del muro de retención, Ww, para desplazamientos tolerables que tengan lugar durante un sismo.

1. Determine el desplazamiento tolerable, Δ, del muro.
2. Obtenga un valor de diseño para Kh, con 

En la ecuación (7.29), Aa y Av son coeficientes de aceleración efectiva Y es el desplazamiento en pulgadas. Las magnitudes de Aa y Av son dadas

Comentarios Relativos a la Estabilidad - Suelos.

Cuando un estrato de suelo débil se localiza cerca de la superficie del terreno, es decir a una profundidad aproximada de 1.5 veces el ancho del muro de retención, la capacidad de carga del estrato débil debe ser investigada cuidadosamente. La posibilidad de un asentamiento excesivo debe también ser considerada. En algunos casos, el uso de un material ligero de relleno detrás del muro de retención resuelve el problema.

En muchos casos se usan pilotes para transmitir la carga de la cimentación a un estrato más firme. Sin embargo, a menudo el empuje de la cuña deslizante de suelo, en el caso de una falla por cortante profunda, flexiona los pilotes haciéndolos fallar. Debe darse una cuidadosa atención a esta posibilidad cuando se considere la opción de una cimentación a base de pilotes para muros de retención. (Cimentaciones con pilotes se requieren en estribos de puentes para evitar el problema de la socavación.)

El coeficiente depresión activa de la tierra se usa para determinar la fuerza lateral del relleno. El estado activo del relleno se establece sólo si el muro cede suficientemente, lo que no sucede en todos los casos. El grado de cedencia del muro dependerá de su altura y de su módulo de sección. Además, la fuerza lateral del relleno dependerá de varios factores, identificados por Casagrande (1973):

a. Efecto de la temperatura
b. Fluctuación del nivel freático
c. Reajuste de las partículas del suelo debido al flujo plástico y lluvia prolongada
d. Cambios en las mareas
e. Fuerte acción de las olas
f. Vibración por tránsito
g. Sismos

Un acomodo insuficiente del muro combinado con otros factores imprevistos genera una fuerza lateral mayor sobre la estructura de retención comparada con la obtenida por la teoría de la presión activa de la tierra. Casagrande (1973) investigó la distribución de la presión lateral de la tierra detrás de un estribo de puente (en Alemania) con relleno de escoria, como muestra la figura 7.17. Las pruebas de laboratorio del relleno de escoria dieron ángulos de fricción de entre 37° y 45º, dependiendo del grado de compactación. Para fines de comparación, la variación de la presión activa de Rankine con Ø=37º y  Ø=45º se muestra también en la figura 7.17. La comparación de los diagramas de presión real y teórica indica: 

 FIGURA 7.18

FIGURA 7.20

Condiciones del filtro

1. D15(F) debe ser menor que 5D85(F), es decir, 5 X 0.25 1.25 mm.
2. D15(F)  debe ser mayor que 4D15(B), es decir, 4 X 0.04 = 0.16 mm.
3. D15(F)  debe ser menor que 25D50(B), es decir, 25 X 0.13 = 3.25 mm.
4. D15(F) debe ser menor que 20D15(B), es decir, 20 X 0.04 = 0.8 mm.
 
Los puntos límite están graficados en la figura 7.20. A través de éstos se dibujan dos curvas que son similares en naturaleza a la curva granulométrica del material del relleno. Esas curvas definen el rango para el material del filtro por usarse.

Otros Tipos de Posibles Fallas en un Muro de Retención.

Además de los tres tipos de posibles fallas en muros de retención vistas anteriormente, otros dos llegan a ocurrir: falla por cortante superficial y falla por cortante profunda.

La falla por cortante supeficia1 en el suelo debajo de la base de un muro de retención tiene lugar a lo largo de una superficie cilíndrica abc que pasa por el talón, como muestra la figura 7.15a. El centro del arco del círculo abc se localiza en O, que se encuentra por tanteos (corresponde al factor de seguridad mínimo). Este tipo de falla ocurre como resultado de un esfuerzo cortante excesivo inducido a lo largo de la superficie cilíndrica en el suelo. En general, el factor de seguridad contra deslizamiento horizontal es menor que el factor de seguridad obtenido mediante falla por cortante superficial. Entonces, si FS(deslizamiento) es mayor que aproximadamente 1.5, la falla por cortante superficial bajo la base puede no ocurrir.

La falla por cortante profunda ocurre a lo largo de una superficie cilíndrica abc, lo muestra la figura 7.15b, como resultado de la existencia de una capa débil de suelo debajo del muro a una profundidad cercana a 1.5 veces el ancho del muro de retención. En tales casos, la superficie de falla cilíndrica crítica abc tiene que ser determinada por

FIGURA 7.16  Análisis de falla por cortante profundo.

  

17. Determine el factor de seguridad contra falla por cortante profunda para esta superficie de falla de tanteo:

Varias superficies de falla por tanteo se dibujan, y el factor de seguridad se determina de manera similar. El valor más bajo del factor de seguridad obtenido de todas las superficies por tanteo es el factor de seguridad deseado.

Muros - Determinar el Factor de seguridad contra volteo, el factor de seguridad contra deslizamiento, la presión sobre el suelo en la punta y talón II.

Resuelva el ESTE EJEMPLO   ejemplo  y  use la presión activa de Coulomb para el cálculo y δ = 2 Ø/3.

Solución: Refiérase a la figura 7.13 para el cálculo de la presión: 

Parte a: Factor de seguridad contra volteo.

Refiérase a las figura 7.14  y  7.12.

 FIGURA 7.13

FIGURA 7.14 

El momento de volteo es 

Por consiguiente, 

Parte b: Factor de seguridad contra deslizamiento 

Parte c: Presión sobre el suelo en la punta y talón

Muro - Determinar el Factor de seguridad contra volteo, el factor de seguridad contra deslizamiento, la presión sobre el suelo en la punta y talón.

En la figura 7.12 se muestra un muro de retención de gravedad de concreto. Determine

a. El factor de
b. El factor de seguridad contra deslizamiento
c. La presión sobre el suelo en la punta y talón

(Nola: Peso unitario del concreto = = 150 lb/pies3.)

Solución: 

 FIGURA 7.12

Parte a: Factor de seguridad contra volteo

La siguiente tabla ahora se prepara para obtener ∑MR:

El momento de volteo 

Parte b: Factor de seguridad contra deslizamiento
De la ec. (7.11), con k1 = k2 = y suponiendo que P = O,

Parte c: Presión sobre el suelo en la punta y en el talón
De las ecs. (7.16), (7.17) y (7.18),

Ejemplo: Calcular la fuerza activa de Coulomb por longitud unitaria del muro

Considere el muro de retención mostrado en la figura 6.12a. Se dan: H = 4.6 m; peso específico del suelo = 16.5 kN/m3 ángulo de fricción del suelo = 30º; ángulo de fricción del muro, δ = 2/3 Ø ; cohesión del suelo, c = 0; α=0 y β=90º Calcule la fuerza activa de Coulomb por longitud unitaria del muro.

Solución: De la ec. (6.25) 

Presión Activa de Tierra de Coulomb.

Los cálculos de la presión activa de tierra de Rankine vistos en las secciones anteriores se basaron en la hipótesis de que el muro no tiene fricción. En 1776, Coulomb propuso una teoría para calcular la presión lateral de la tierra sobre un muro de retención con relleno de suelo granular, tomando en cuenta la fricción del muro.

Para aplicar la teoría de la presión activa de Coulomb, considérese un muro de retención con su espalda inclinada un ángulo β respecto a la horizontal, como muestra la figura 6.12a. El relleno es un suelo granular que se inclina un ángulo α con la horizontal y s es el ángulo de fricción entre el suelo y el muro (es decir, el ángulo de fricción del muro).

Bajo presión activa, el miro se moverá alejándose de la masa del suelo (hacia la izquierda en la figura 6.12a). Coulomb supuso que, en tal caso, la superficie de falla en el suelo sería un plano (por ejemplo, BC1, BC2,...). Entonces, para hallar la fuerza activa 

 FIGURA 6.12 Presión activa de Coulomb

 

 

en el ejemplo, considérese una posible cuña de falla de suelo ABC1. Las fuerzas que actúan sobre esta cuña ABC1 (por unidad de longitud en ángulo recto a la sección transversal mostrada), son las siguientes:

1. El peso W de la cuña.
2. La resultante, R, de las fuerzas normales y cortantes resistentes a lo largo de la superficie BC1. La fuerza R estará inclinada un ángulo Ø respecto a la normal a la superficie BC1.
3. La fuerza activa por longitud unitaria del muro, Pa. La fuerza Pa estará inclinada un ángulo S respecto a la normal al respaldo del muro.

Para fines de equilibrio, un triángulo de fuerzas se dibuja como muestra la figura 6.12b. Note que θ1 es el ángulo que BC1 forma con la horizontal. Como la magnitud de W así como las direcciones de las tres fuerzas son conocidas, el valor de Pa ahora es determinado. Similarmente, las fuerzas activas de otras cuñas de prueba, tales como las ABC2, ABC3,... se determinan. El valor máximo de Pa así calculado es la fuerza activa de Coulomb (véase la parte superior de la figura 6.12), que se expresa como 

donde 

Muestra la figura 6.13, la fuerza activa, Pa se calcula como

FIGURA 6.13  Presión activa de Coulomb con sobrecarga sobre el relleno.

donde

Descargar :

 

Descargar:

Ejemplo: Cálculo de la fuerza activa de Rankine por unidad de longitud del muro y la localización de la resultante después de que ocurre la grieta de tensión.

Refiérase al muro de retención mostrado en la figura 6.10. Se dan: H = 7.5 m, y = 18 kN/m3, Ø = 20º, c = 13.5 kN/m2 y α = 100. Calcule la fuerza activa de Rankine, Pa, por unidad de longitud del muro y la localización de la resultante después de que ocurre la grieta de tensión. 

Solución de la Ec 6.24.

FIGURA 6.11

Presión Activa de Tierra de Rankine para Terraplén Inclinado.

Si el relleno de un muro sin fricción es un suelo granular (c = O) y se eleva con un ángulo α con respecto a la horizontal (figura 6.10), el coeficiente de presión activa de la tierra, Ka, se expresa en la forma 

donde Ø =  ángulo de fricción del suelo

A cualquier profundidad z, la presión activa de Rankine se expresa como

 
La fuerza total por unidad de longitud del muro es 

 

FIGURA 6.10 Notación para la presión activa; ecs. (6.19), (6.20) y (6.21)

Note que en este caso, la dirección de la fuerza resultante, Pa, está inclinada a un ángulo α con ki horizontal y cruza el muro a una distancia de H/3 desde la base del muro. La tabla 6,2 presenta los valores de Ka (presión activa de la tierra) para varios valores α y Ø.

El análisis anterior se extiende a un relleno inclinado con un suelo c—Ø. Los detalles de la derivación matemática están dados por Mazindrani y Ganjali (1997). Como en la ecuación (6.20), para este caso

TABLA 6.2 Coeftciente K0 [ec. (6.19)] de presión activa de la tierra 

 

 

TABLA Valores de K' a

donde

Algunos valores de K’a se dan en la tabla  6.3. Para un problema de este tipo, la profundidad de la grieta de tensión, zc, se da por